Statistical Significance Script For Google Analytics

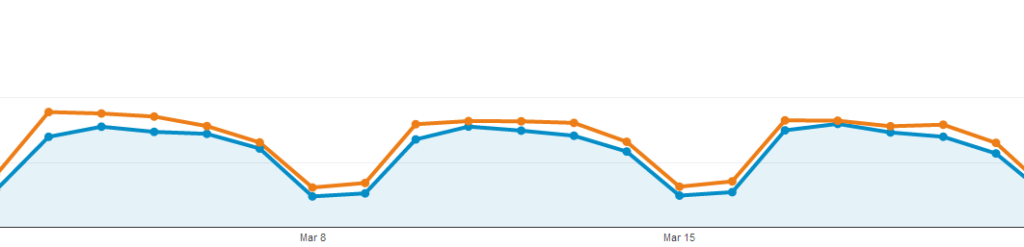
When comparing two time periods in Google Analytics, we are given a percentage increase or decrease. In situations where there is a dramatic difference (as is often the case for year-over-year comparisons), we can safely assume that the result is statistically significant.

For example, in the below chart, every data point (day) is lower in the second period than in the first. We can reasonably conclude that there has been an increase in visits in our month-over-month comparison.

Clear Trend in Google Analytics

When we have a more-subtle increase (decrease) in a time comparison, however, the percentage increase (decrease) may not actually be statistically significant. This script will evaluate the graph’s data and determine whether (and at what level) the percentage change is statistically significant

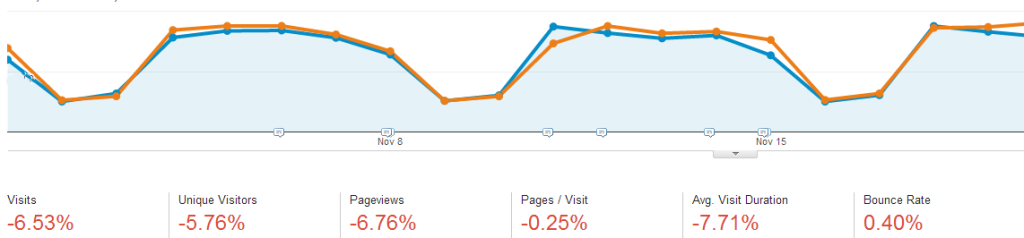
Unclear Trend in Google Analytics

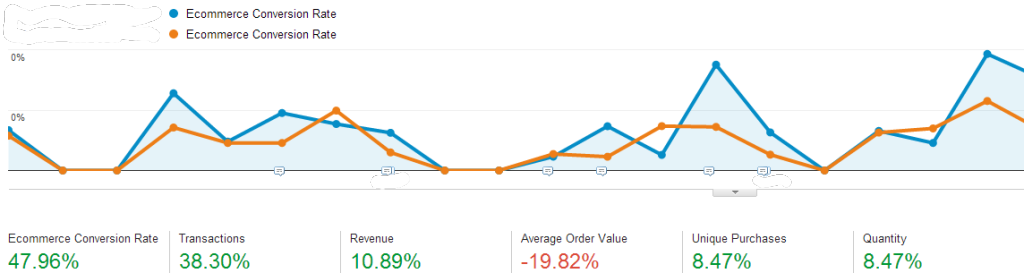
Unclear Trend in Google Analytics E-Commerce

This should be considered a Beta script. It has several limitations at this time, but they will be removed (hopefully) soon as I have time. Eventually I plan to release this as a Chrome Extension in the Google Marketplace.

Directions

1. Set the date range and compare to date range such that they each have the same number of days, weeks, or months (6 to 40) and begin and end on the same weekday.
2. On the graph, use the dropdown for the metric you want to test
3. Copy and paste the Script into your developer console (F12 opens the developer console).
4. The result of the test will be output to the developer console.

Script Limitations

1. You must use comparable time periods in terms of Days of the week. If your date range starts on Monday and ends on a Friday and is 26 days, then the previous date range should also start on a Monday, end on a Friday, and be 26 days.
2. Must use between 6 and 40 data points. If the graph is displaying days, between 6 and 40 days. If the graph is displaying months, between 6 and 40 months
3. The script only determines if the percentage change is insignificant, or significant at 10%, 5%, or 1% level (p-values of 0.10, 0.05, or 0.01)
4. Currently, the Script uses the Wilcoxon paired rank test. We lose power by not treating the data as a time series, and we make several other approximations. For greater than 40 data points, we can use a t-test to evaluate the significance of the percentage change displayed in the graph. This will be added in the next release.

(function(){

//load jQuery
jq = document.createElement('script');
jq.src = "//ajax.googleapis.com/ajax/libs/jquery/1/jquery.min.js";
document.getElementsByTagName('head')[0].appendChild(jq);

//call main once jQuery is ready
setTimeout(function(){
	jQuery.noConflict();
	datas = statMain();
},1000);

function statMain(){
	var m1 = 139.5232, b1 = 59.24425, diff = sign = testW = 0; //testW is the Wilcoxon statistic
	var dataFrame = [];
	var rankHolder = [];
	var graphTarget = "";

	//check if overview or explorer graph present
	if(jQuery("#ID-explorer-graph-lineChart").length > 0){
		graphTarget = "#ID-explorer-graph-lineChart";
	} else if(jQuery("#ID-overview-graph-lineChart").length > 0){
		graphTarget = "#ID-overview-graph-lineChart";
	}

	var currCircles = 	jQuery(graphTarget+" svg>g:eq(0)>g:eq(1)>circle[fill='#058dc7']");
	var pastCircles = 	jQuery(graphTarget+" svg>g:eq(0)>g:eq(1)>circle[fill='#ed7e17']");
	var numPoints = currCircles.length;
	var scaleBy = temp = jQuery(graphTarget+" svg text:last").text();
	scaleBy = scaleBy.replace(",","");
	scaleBy = parseInt(scaleBy);

	//y2 is for current timeframe
	//y1 is for past timeframe
	for(var i = 0; i < numPoints; i++){

		var y2 = (m1 - jQuery(currCircles).eq(i).attr('cy'))*b1/8000*scaleBy;
		var y1 = (m1 - jQuery(pastCircles).eq(i).attr('cy'))*b1/8000*scaleBy;
		var diff = Math.abs(y2-y1);
		var sign = (y2-y1)?(y2-y1)<0?-1:1:0;
		dataFrame[i] = [y2,y1,diff,sign];

		//for the wilcoxon computation
		rankHolder[i] = i+1;
	}

	//compute wilcoxon sign test statistic

	//sort on the abs diff
	dataFrame.sort(function(a,b){return a[2] - b[2]});

	for(var i = 0; i < numPoints; i++){ 		if(dataFrame[i][3]>0){
			testW+=dataFrame[i][3]*rankHolder[i];
		}
	}
	testW=numPoints*(numPoints+1)/2 - testW;

	console.log("test statistic:" +testW);

	//look up p-value based on testW and n = sample size
	if(numPoints == 0){
		console.log("Error - graph not able to be read");
	}else if(numPoints < 6){
            console.log("Sample size not large enough to conduct test");
        } else{
            console.log("This test is based on "+numPoints+" samples.");
            var isSig = lookUpSignificance(testW,numPoints);
            console.log("P-value is "+isSig+ " for "+ jQuery(".ID-primaryConcept .ID-buttonText").text());
 	}
return dataFrame;
}

function lookUpSignificance(testW,numPoints){
        var alphaValues = ["0.10","0.05","0.01"];
        var significance = "greater than 0.10, so no significant difference";
        if(numPoints > 5 && numPoints <41){
		var testRow = lookupTable[numPoints-6];

		for(var i=1;i<alphaValues.length;i++){
			if(testW <= testRow[alphaValues[i]]){
				significance = alphaValues[i];
			}
		}

	}
	return significance;
}

//json key is for α value, except for df
var lookupTable =
[{"df":6,"0.10":2,"0.05":.5,"0.01":0},
{"df":7,"0.10":3,"0.05":2,"0.01":0},
{"df":8,"0.10":5,"0.05":3,"0.01":0},
{"df":9,"0.10":8,"0.05":5,"0.01":1},
{"df":10,"0.10":10,"0.05":8,"0.01":3},
{"df":11,"0.10":13,"0.05":10,"0.01":5},
{"df":12,"0.10":17,"0.05":13,"0.01":7},
{"df":13,"0.10":21,"0.05":17,"0.01":9},
{"df":14,"0.10":25,"0.05":21,"0.01":12},
{"df":15,"0.10":30,"0.05":25,"0.01":15},
{"df":16,"0.10":35,"0.05":29,"0.01":19},
{"df":17,"0.10":41,"0.05":34,"0.01":23},
{"df":18,"0.10":47,"0.05":40,"0.01":27},
{"df":19,"0.10":53,"0.05":46,"0.01":32},
{"df":20,"0.10":60,"0.05":52,"0.01":37},
{"df":21,"0.10":67,"0.05":58,"0.01":42},
{"df":22,"0.10":75,"0.05":65,"0.01":48},
{"df":23,"0.10":83,"0.05":73,"0.01":54},
{"df":24,"0.10":91,"0.05":81,"0.01":61},
{"df":25,"0.10":100,"0.05":89,"0.01":68},
{"df":26,"0.10":110,"0.05":98,"0.01":75},
{"df":27,"0.10":119,"0.05":107,"0.01":83},
{"df":28,"0.10":130,"0.05":116,"0.01":91},
{"df":29,"0.10":140,"0.05":126,"0.01":100},
{"df":30,"0.10":151,"0.05":137,"0.01":109},
{"df":31,"0.10":163,"0.05":147,"0.01":118},
{"df":32,"0.10":175,"0.05":159,"0.01":128},
{"df":33,"0.10":187,"0.05":170,"0.01":138},
{"df":34,"0.10":200,"0.05":182,"0.01":148},
{"df":35,"0.10":213,"0.05":195,"0.01":159},
{"df":36,"0.10":227,"0.05":208,"0.01":171},
{"df":37,"0.10":241,"0.05":221,"0.01":182},
{"df":38,"0.10":256,"0.05":235,"0.01":194},
{"df":39,"0.10":271,"0.05":249,"0.01":207},
{"df":40,"0.10":286,"0.05":264,"0.01":220}];

})()

I think it is important for us to incorporate statistical testing into our Google Analytics. Especially when there exists a subtle change in our data over time, we risk committing a type I error (false positive) and incorrectly appropriating our organization’s resources based on the faulty intelligence.