Forecasting with a Time Series Model using Python: Part Two

Now for the exciting part: modeling!

In Part One of this two-part series, we walked through the steps for understanding and preparing your data for time series modeling. In Part Two, we will take a look at four prediction models: Simple Exponential Smoothing (SES), Holt, Seasonal Holt-Winters, and Seasonal ARIMA (SARIMA). Then we will evaluate these forecasting models to determine which is best for our sample dataset.

Remember that all the code referenced in this post is available here on Github. Please feel free to use it and share your feedback or questions.

Choosing a Time Series Prediction Model

Before we walk through the various models, I want to make an important point: Not all of these models are suitable for the sample dataset we’re using in this blog post. But, I am walking through them anyway to describe some of the options, and to show how and why not all models are appropriate for all datasets.

The appropriate model for your time-series data will depend on the data’s particular characteristics, for example, if the dataset has an overall trend or seasonality. Please be sure to choose the model that best suits your data.

To help us evaluate the performance of each forecasting model, we need to measure the differences between predicted values and the actual or observed values. For the models I present below, I used the commonly-used measurement metric root-mean-square error (RMSE) also referred to as root-mean-square deviation (RMSD).

Other measures commonly used are forecast error, mean absolute error (MAE), and mean absolute percentage error (MAPE). When testing more than one model, be sure to use the same performance metric consistently across all of them. 

Now let’s consider four forecasting models:

• Simple Exponential Smoothing (SES) for data without trend or seasonality
• Holt’s Linear Trend Method for data with a trend but no seasonality
• Holt-Winters’ Seasonal Method for data with trend and/or seasonality
• SARIMA for data with trend and/or seasonality

Simple Exponential Smoothing (SES)

Suitable for time series data without trend or seasonal components

This model calculates the forecasting data using weighted averages. One important parameter this model uses is the smoothing parameter: α, and you can pick a value between 0 and 1 to determine the smoothing level. When α = 0, the forecasts are equal to the average of the historical data. When α = 1, the forecasts will be equal to the value of the last observation.

You can either choose a specific α (e.g., in the sample code, I used 0.8) or use the Python ‘statsmodels’ module to automatically find an optimized value for the dataset. I usually use the auto-optimization approach which gives us the lowest error, but if you want to be more conservative or aggressive, you can specify α.

import numpy as np
from statsmodels.tsa.api import SimpleExpSmoothing 

def ses(y, y_to_train,y_to_test,smoothing_level,predict_date):
    y.plot(marker='o', color='black', legend=True, figsize=(14, 7))
    
    fit1 = SimpleExpSmoothing(y_to_train).fit(smoothing_level=smoothing_level,optimized=False)
    fcast1 = fit1.forecast(predict_date).rename(r'$\alpha={}$'.format(smoothing_level))
    # specific smoothing level
    fcast1.plot(marker='o', color='blue', legend=True)
    fit1.fittedvalues.plot(marker='o',  color='blue')
    mse1 = ((fcast1 - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of our forecasts with smoothing level of {} is {}'.format(smoothing_level,round(np.sqrt(mse1), 2)))
    
    ## auto optimization
    fit2 = SimpleExpSmoothing(y_to_train).fit()
    fcast2 = fit2.forecast(predict_date).rename(r'$\alpha=%s$'%fit2.model.params['smoothing_level'])
    # plot
    fcast2.plot(marker='o', color='green', legend=True)
    fit2.fittedvalues.plot(marker='o', color='green')
    
    mse2 = ((fcast2 - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of our forecasts with auto optimization is {}'.format(round(np.sqrt(mse2), 2)))
    
    plt.show()

ses(y, y_to_train,y_to_val,0.8,predict_date)

The visualization of the results for the simple exponential smoothing (SES) forecast model shows the difference between the specified α (blue line) and the auto-optimized α (green line). As you can see from the graph, SES will predict a flat, forecasted line since the logic behind it uses weighted averages. Even though the RMSE is low, it does not predict any fluctuation. Since most time series data has some kind of trend or seasonality, this model can be used to get a sense of a baseline for comparison. 

Holt’s Linear Trend Method

Suitable for time series data with a trend component but without a seasonal component 

Expanding the SES method, the Holt method helps you forecast time series data that has a trend. In addition to the level smoothing parameter α introduced with the SES method, the Holt method adds the trend smoothing parameter β*. Like with parameter α, the range of β* is also between 0 and 1.

The sample code below contains two different variants within the Holt method. Both fits have the α = 0.6, β* = 0.2 as parameter values. The fit1 is the default Holt’s additive model, and the fit2 is an exponential model. An exponential model would be appropriate for situations where the increase or decrease starts slowly but then accelerates rapidly.

from statsmodels.tsa.api import Holt

def holt(y,y_to_train,y_to_test,smoothing_level,smoothing_slope, predict_date):
    y.plot(marker='o', color='black', legend=True, figsize=(14, 7))
    
    fit1 = Holt(y_to_train).fit(smoothing_level, smoothing_slope, optimized=False)
    fcast1 = fit1.forecast(predict_date).rename("Holt's linear trend")
    mse1 = ((fcast1 - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of Holt''s Linear trend {}'.format(round(np.sqrt(mse1), 2)))

    fit2 = Holt(y_to_train, exponential=True).fit(smoothing_level, smoothing_slope, optimized=False)
    fcast2 = fit2.forecast(predict_date).rename("Exponential trend")
    mse2 = ((fcast2 - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of Holt''s Exponential trend {}'.format(round(np.sqrt(mse2), 2)))
    
    fit1.fittedvalues.plot(marker="o", color='blue')
    fcast1.plot(color='blue', marker="o", legend=True)
    fit2.fittedvalues.plot(marker="o", color='red')
    fcast2.plot(color='red', marker="o", legend=True)

    plt.show()

holt(y, y_to_train,y_to_val,0.6,0.2,predict_date)

Looking at the visualization for the Holt method, we see how the linear trend (blue line) and exponential trend (red line) compare to each other and to the order volumes. Compared with SES, Holt captures more of the trend of the data. However, as you can see from the visual, the trend it discovered is too dramatic and would be very unlikely to take place in real life.

Holt-Winters’ Seasonal Method

Suitable for time series data with trend and/or seasonal components

The Holt-Winters model extends Holt to allow the forecasting of time series data that has both trend and seasonality, and this method includes this seasonality smoothing parameter: γ.

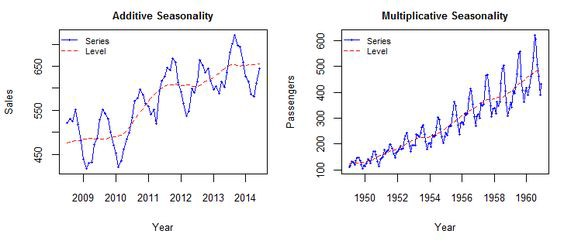
There are two general types of seasonality: Additive and Multiplicative. 

• Additive: xt = Trend + Seasonal + Random
  
  Seasonal changes in the data stay roughly the same over time and don’t fluctuate in relation to the overall data.
• Multiplicative: xt = Trend * Seasonal * Random
  
  The seasonal variation changes in relation to the overall changes in the data. So, if the data is trending upward, the seasonal differences grow proportionally as well.

Here’s a helpful visual:

^{Source: Sigmundo Preissler Jr, PhD}

Once you figure out which type of seasonality you’re dealing with in your data, you can identify the frequency of seasonality or m. For data with a quarterly seasonal pattern, m = 4, while for a monthly seasonal data pattern, m = 12. Our sample data has a yearly seasonal pattern with 2 years of data, and we aggregated it by week, so each data point is one week, so m = 52.

The Python statsmodels module provides users with a range of parameter combinations based on the trend types, seasonality types, and other options for doing Box-Cox transformations. This package is kind of like the time series version of grid search for hyperparameter tuning. To find out more, see this documentation and this detailed explanation to help you choose the one that suits your data best.

from statsmodels.tsa.api import ExponentialSmoothing

def holt_win_sea(y,y_to_train,y_to_test,seasonal_type,seasonal_period,predict_date):
    
    y.plot(marker='o', color='black', legend=True, figsize=(14, 7))
    
    if seasonal_type == 'additive':
        fit1 = ExponentialSmoothing(y_to_train, seasonal_periods = seasonal_period, trend='add', seasonal='add').fit(use_boxcox=True)
        fcast1 = fit1.forecast(predict_date).rename('Additive')
        mse1 = ((fcast1 - y_to_test) ** 2).mean()
        print('The Root Mean Squared Error of additive trend, additive seasonal of '+ 
              'period season_length={} and a Box-Cox transformation {}'.format(seasonal_period,round(np.sqrt(mse1), 2)))
        
        fit2 = ExponentialSmoothing(y_to_train, seasonal_periods = seasonal_period, trend='add', seasonal='add', damped=True).fit(use_boxcox=True)
        fcast2 = fit2.forecast(predict_date).rename('Additive+damped')
        mse2 = ((fcast2 - y_to_test) ** 2).mean()
        print('The Root Mean Squared Error of additive damped trend, additive seasonal of '+ 
              'period season_length={} and a Box-Cox transformation {}'.format(seasonal_period,round(np.sqrt(mse2), 2)))
        
        fit1.fittedvalues.plot(style='--', color='red')
        fcast1.plot(style='--', marker='o', color='red', legend=True)
        fit2.fittedvalues.plot(style='--', color='green')
        fcast2.plot(style='--', marker='o', color='green', legend=True)
    
    elif seasonal_type == 'multiplicative':  
        fit3 = ExponentialSmoothing(y_to_train, seasonal_periods = seasonal_period, trend='add', seasonal='mul').fit(use_boxcox=True)
        fcast3 = fit3.forecast(predict_date).rename('Multiplicative')
        mse3 = ((fcast3 - y_to_test) ** 2).mean()
        print('The Root Mean Squared Error of additive trend, multiplicative seasonal of '+ 
              'period season_length={} and a Box-Cox transformation {}'.format(seasonal_period,round(np.sqrt(mse3), 2)))
        
        fit4 = ExponentialSmoothing(y_to_train, seasonal_periods = seasonal_period, trend='add', seasonal='mul', damped=True).fit(use_boxcox=True)
        fcast4 = fit4.forecast(predict_date).rename('Multiplicative+damped')
        mse4 = ((fcast3 - y_to_test) ** 2).mean()
        print('The Root Mean Squared Error of additive damped trend, multiplicative seasonal of '+ 
              'period season_length={} and a Box-Cox transformation {}'.format(seasonal_period,round(np.sqrt(mse4), 2)))
        
        fit3.fittedvalues.plot(style='--', color='red')
        fcast3.plot(style='--', marker='o', color='red', legend=True)
        fit4.fittedvalues.plot(style='--', color='green')
        fcast4.plot(style='--', marker='o', color='green', legend=True)
        
    else:
        print('Wrong Seasonal Type. Please choose between additive and multiplicative')

    plt.show()

holt_win_sea(y, y_to_train,y_to_val,'additive',52, predict_date)

The visualization of the results for the Holt-Winters method shows the additive (red line) compared to the additive + damped (green line) trends. Based on the visualization, we see that the Holt-Winters model fits the actual data best, so far. However, the RMSE is not better than the results from the simple SES model. And we can also tell that the forecast starts to drop off towards the end.

SARIMA

Suitable for time series data with trend and/or seasonal components

While exponential smoothing models use weighted averages of past observations to forecast new values, Auto-Regressive Integrated Moving Average or ARIMA models look at autocorrelations or serial correlations in the data. In other words, ARIMA models look at differences between values in the time series. You can learn more about ARIMA models here. SARIMA builds upon the concept of ARIMA but extends it to model the seasonal elements in your data. 

 

You’ll notice that SARIMA includes several parameters that can be tuned to achieve optimal performance. You can learn more about these parameters here. They are:

 

Trend Elements:

• p: Trend autoregression order.
• d: Trend difference order.
• q: Trend moving average order.

Seasonal Elements:

• P: Seasonal autoregressive order.
• D: Seasonal difference order.
• Q: Seasonal moving average order.
• m: The number of time steps for a single seasonal period.

In order to get the best prediction, it’s important to find the values of SARIMA(p,d,q)(P,D,Q)m that optimize a metric of interest. For the purposes of this brief blog post, we will just use a "grid search" to iteratively explore different combinations of parameters. Learn more about grid search.

The evaluation metric we’ll use for the grid search is the AIC (Akaike Information Criterion) value. The AIC measures how well a model fits the data while taking into account the overall complexity of the model. In general, we want to pick the combination with the lowest AIC value.

import itertools

def sarima_grid_search(y,seasonal_period):
    p = d = q = range(0, 2)
    pdq = list(itertools.product(p, d, q))
    seasonal_pdq = [(x[0], x[1], x[2],seasonal_period) for x in list(itertools.product(p, d, q))]
    
    mini = float('+inf')
    
    
    for param in pdq:
        for param_seasonal in seasonal_pdq:
            try:
                mod = sm.tsa.statespace.SARIMAX(y,
                                                order=param,
                                                seasonal_order=param_seasonal,
                                                enforce_stationarity=False,
                                                enforce_invertibility=False)

                results = mod.fit()
                
                if results.aic < mini:
                    mini = results.aic
                    param_mini = param
                    param_seasonal_mini = param_seasonal

#                 print('SARIMA{}x{} - AIC:{}'.format(param, param_seasonal, results.aic))
            except:
                continue
    print('The set of parameters with the minimum AIC is: SARIMA{}x{} - AIC:{}'.format(param_mini, param_seasonal_mini, mini))

sarima_grid_search(y,52)

The grid search tested all possible combinations of variables, and printed out the set that resulted in the lowest AIC, and we can see that SARIMA(1, 1, 1)x(1, 1, 0, 52) has the lowest AIC value. Since this method chose the best parameters, we will use this method to fit our model and compare the results with all the previous models discussed above.

# Call this function after pick the right(p,d,q) for SARIMA based on AIC               
def sarima_eva(y,order,seasonal_order,seasonal_period,pred_date,y_to_test):
    # fit the model 
    mod = sm.tsa.statespace.SARIMAX(y,
                                order=order,
                                seasonal_order=seasonal_order,
                                enforce_stationarity=False,
                                enforce_invertibility=False)

    results = mod.fit()
    print(results.summary().tables[1])
    
    results.plot_diagnostics(figsize=(16, 8))
    plt.show()
    
    # The dynamic=False argument ensures that we produce one-step ahead forecasts, 
    # meaning that forecasts at each point are generated using the full history up to that point.
    pred = results.get_prediction(start=pd.to_datetime(pred_date), dynamic=False)
    pred_ci = pred.conf_int()
    y_forecasted = pred.predicted_mean
    mse = ((y_forecasted - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of SARIMA with season_length={} and dynamic = False {}'.format(seasonal_period,round(np.sqrt(mse), 2)))

    ax = y.plot(label='observed')
    y_forecasted.plot(ax=ax, label='One-step ahead Forecast', alpha=.7, figsize=(14, 7))
    ax.fill_between(pred_ci.index,
                    pred_ci.iloc[:, 0],
                    pred_ci.iloc[:, 1], color='k', alpha=.2)

    ax.set_xlabel('Date')
    ax.set_ylabel('Sessions')
    plt.legend()
    plt.show()

    # A better representation of our true predictive power can be obtained using dynamic forecasts. 
    # In this case, we only use information from the time series up to a certain point, 
    # and after that, forecasts are generated using values from previous forecasted time points.
    pred_dynamic = results.get_prediction(start=pd.to_datetime(pred_date), dynamic=True, full_results=True)
    pred_dynamic_ci = pred_dynamic.conf_int()
    y_forecasted_dynamic = pred_dynamic.predicted_mean
    mse_dynamic = ((y_forecasted_dynamic - y_to_test) ** 2).mean()
    print('The Root Mean Squared Error of SARIMA with season_length={} and dynamic = True {}'.format(seasonal_period,round(np.sqrt(mse_dynamic), 2)))

    ax = y.plot(label='observed')
    y_forecasted_dynamic.plot(label='Dynamic Forecast', ax=ax,figsize=(14, 7))
    ax.fill_between(pred_dynamic_ci.index,
                    pred_dynamic_ci.iloc[:, 0],
                    pred_dynamic_ci.iloc[:, 1], color='k', alpha=.2)

    ax.set_xlabel('Date')
    ax.set_ylabel('Sessions')

    plt.legend()
    plt.show()
    
    return (results)

Here are the visualizations for the SARIMA method. Compared with the results of all the previous models, we can be confident saying the SARIMA model best captures both the seasonality and trend of our dataset. Its forecasted results are closest to the actual sales.

In addition to using the Root Mean Squared Error (RMSE) metric, I also ran plot_diagnostics( ), which is a really valuable function to ensure that none of the assumptions made by the model have been violated, and that there is no unusual behavior. The dynamic=False argument ensures that we produce one-step-ahead forecasts, meaning that forecasts at each point are generated using the full history up to that point. Unfortunately, this is a function that can only be built inside the SARIMA and ARIMA packages, so we cannot print out the same results for the other models we have considered.

model = sarima_eva(y,(1, 1, 1),(1, 1, 0, 52),52,'2019-06-02',y_to_val)

There are a few things to check to help you get the most out of these diagnostic graphs:

1. The top left plot shows the residuals over time. We do not want to see any obvious seasonality here and the messier it is, the better we can say we found the trend and seasonality in our data and removed the noise.

2. In the top-right plot, we want to see that the red KDE line follows closely with the N(0,1) line to indicate that the residuals are normally distributed. This line is the standard notation for a normal distribution with a mean of 0 and a standard deviation of 1.

3. In the bottom left qq-plot, you see the ordered distribution of residuals (blue dots) following the linear trend (red line) of the samples taken from a standard normal distribution with N(0, 1).

4. The autocorrelation visual (called a “correlogram”) on the bottom right shows that the time series residuals have a low correlation with the lagged versions of itself (that is, the majority of dots fall into the blue shaded area).

By validating all the four points above, we can conclude that this model’s residuals are near normally distributed. This indicates we have found a well-fit model suitable for our dataset.

If we were only concerned with achieving the lowest Root Mean Squared Error, we would choose the Simple Exponential Smoothing (SES) model to use since it produced the smallest error. In many business cases where longer-term forecasting with more nuanced visualizations are needed in our overall analysis, the SARIMA model is preferred. 

Making Predictions

Now that we have a well-fit model, let’s do some forecasting!

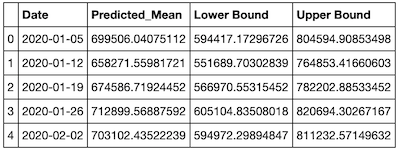
To get the forecast for sales in the next year, we enter steps=52. The results produce both a table showing the Predicted_Mean, Lower Bound and Upper Bound, and the prediction graphs.

def forecast(model,predict_steps,y):
    
    pred_uc = model.get_forecast(steps=predict_steps)

    #SARIMAXResults.conf_int, can change alpha,the default alpha = .05 returns a 95% confidence interval.
    pred_ci = pred_uc.conf_int()

    ax = y.plot(label='observed', figsize=(14, 7))
#     print(pred_uc.predicted_mean)
    pred_uc.predicted_mean.plot(ax=ax, label='Forecast')
    ax.fill_between(pred_ci.index,
                    pred_ci.iloc[:, 0],
                    pred_ci.iloc[:, 1], color='k', alpha=.25)
    ax.set_xlabel('Date')
    ax.set_ylabel(y.name)

    plt.legend()
    plt.show()
    
    # Produce the forcasted tables 
    pm = pred_uc.predicted_mean.reset_index()
    pm.columns = ['Date','Predicted_Mean']
    pci = pred_ci.reset_index()
    pci.columns = ['Date','Lower Bound','Upper Bound']
    final_table = pm.join(pci.set_index('Date'), on='Date')
    
    return (final_table)

You can see from the visualization that our model clearly captured the seasonality as well as the increasing trend of the sales.

final_table = forecast(model,52,y)
final_table.head()

The green line in the graph represents the expected future data based on the forecasting model we built. The green line represents the average forecasted value for each week, and we would not be surprised to see the actual numbers track to this line for the most part. But there is no guarantee of this!

The gray area above and below the green line represents the 95 percent confidence interval and as with virtually all forecasting models, as the predictions go further into the future, the less confidence we have in our values. In this case, we are 95 percent confident that the actual sales will fall inside this range. But, there is a chance the actuals could fall completely outside this range also. The larger the future time period for which we want to predict, the larger this confidence range will be (that is, the less precise our forecast is).

When sharing results with stakeholders, be sure they understand what the confidence interval really means and why it’s important. The results should not be seen as a guaranteed or even expected result, but only as a reference that provides a general picture of the yearly pattern. Lots of uncontrolled factors may heavily influence real-life sales. The sudden onset and huge impacts of COVID-19 present a perfect example of unexpected factors affecting future sales.

Conclusion

Time series analysis and prediction is a huge and fascinating area with a wide range of complexity and applications. The goal of this blog was to introduce you to the general steps data scientists take to analyze and forecast using time series data. 

I hope this provides you with a solid introduction and guide, and that it answers some of the questions you may have when facing the time series for the first time. I encourage you to continue exploring with time series analyses!

All the code referenced in this post is available here on Github. Please feel free to use it and share your feedback or questions.